Ein Blick hinter den quantenmechanischen Vorhang

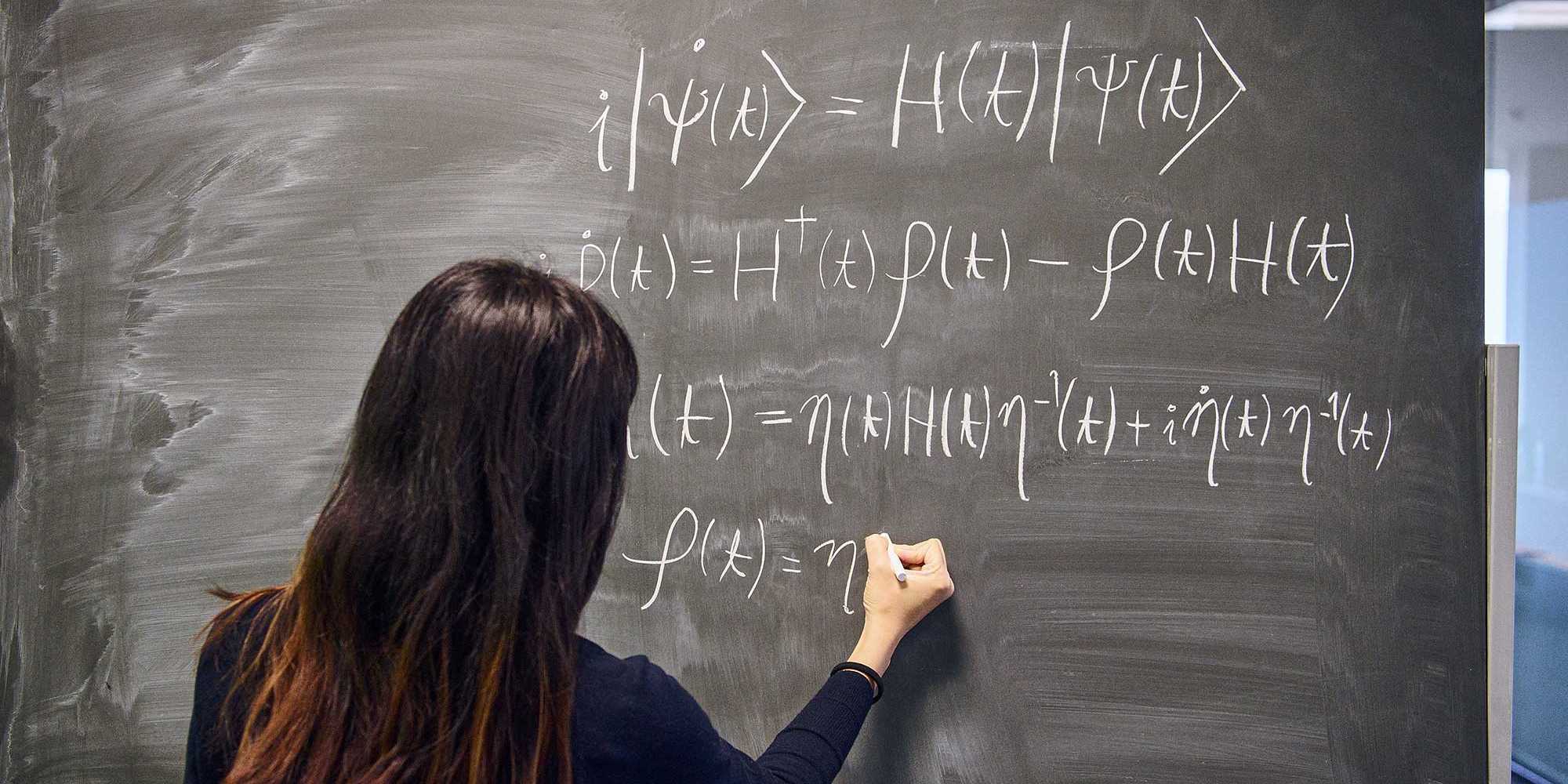
Die Theorie der Quantenmechanik (QM) ist noch lange nicht zu Ende: Seit den Anfängen ihrer Entwicklung hat sie Fragen und Diskussionen über ihre mathematischen Grundlagen und Interpretationen ausgelöst. In der Standard-QM werden Observablen - d. h. physikalische Eigenschaften eines Quantensystems, die gemessen werden können - durch hermitesche Operatoren beschrieben, die reelle Spektren sowie vollständige und orthogonale Sätze von Eigenvektoren haben. Durch die Arbeit mit hermiteschen Operatoren und Hamiltonoperatoren, werden entscheidende Aspekte der Theorie, wie z. B. die Auswirkungen von Messungen, sehr gut erfasst. Die Anforderungen an hermitesche Hamiltonoperatoren sind jedoch nicht in Stein gemeisselt. Tatsächlich haben nun Forschende untersucht, was passiert, wenn diese nicht gestellt sind und die Nicht-Hermitizität zu einer nicht-einheitlichen Zeitentwicklung und komplexen Eigenwerten führen kann.

Wie die bereits im Labor beobachteten unkonventionellen Phänomene zeigen, bieten nicht-hermitesche Systeme eine interessante Spielwiese für neue Physik. Abseits des Labors arbeiten Theoretiker an der Erstellung konsistenter mathematischer Formulierungen der nicht-hermiteschen Quantenmechanik. Karin Sim, ihre Doktormutter Dr. Ramasubramanian Chitra und ihre Kollegen von der ETH Zürich und der Universität Stockholm haben nun ein System für die nicht-hermitesche QM erprobt, das auf einem spezifischen zeitabhängigen Operator, der so genannten Quantenmetrik, basiert. Ihre Ergebnisse, die kürzlich in Physical Review Letters veröffentlicht wurden, werfen ein neues Licht auf grundlegende Aspekte der quantenmechanischen Theorie und die Folgen der Nicht-Hermitizität.

Eine Quantenmetrik

Sim und Kollegen betrachten einen nicht-stationären Hilbertraum mit einem zeitabhängigen, positiv-definiten Operator ρ, der es ermöglicht, diesen Hilbertraum, in dem die zeitliche Entwicklung eines Systems durch einen nicht-hermiteschen Hamiltonoperator erzeugt wird, auf einen anderen Hilbertraum abzubilden, in dem der Hamiltonoperator hermetisch ist und die Nicht-Hermitizität in ρ kodiert ist. Es stellt sich heraus, dass die Rolle des metrischen Operators ρ bei der Untersuchung von nicht-hermiteschen Systemen alles andere als einfach ist, wie die Forscher in dem Papier zeigen.

Nach der Einführung der Metrik und der Erläuterung, wie der Erwartungswert der Beobachtungsgrösse eines Systems zu berechnen ist, betrachten Sim und Kollegen eine Sammlung von zweistufigen nicht-hermiteschen Systemen, die durch den Impuls k parametrisiert und in der Zeit angetrieben werden. Das Interessante an dieser Art von System ist, dass es exakt lösbar ist, was bedeutet, dass seine zeitliche Entwicklung zwischen den beiden hermiteschen asymptotischen Grenzen analytisch untersucht werden kann. Innerhalb des von den Forschern vorgeschlagenen metrischen Rahmens soll die zeitliche Entwicklung des Systems untersucht werden, wenn die Paritäts-Zeit-Symmetrie (PT) – die die Kombination von räumlicher Reflexion und Zeitumkehroperationen beschreibt - erhalten bleibt oder spontan gebrochen wird. Für diese Art von parametrisierten Systemen gibt es in der Tat Singularitäten im Parameterraum, an denen die PT-Symmetrie bricht. An diesen Singularitäten, die als Ausnahmepunkte bekannt sind, verschmelzen zwei oder mehr Eigenwerte und ihre entsprechenden Eigenvektoren.

Als ersten Prüfstand für das metrische System untersuchen Sim und Kollegen die Entwicklung des normalisierten Zustands des Systems und finden bemerkenswerte Diskrepanzen zwischen den Vorhersagen mit und ohne Metrik für bestimmte Parameterregime. Im metrischen System werden die Erwartungswerte der Observablen mit ρ gewichtet und bildeten physikalisch sinnvolle zeitabhängige Erwartungswerte. Bei einem alternativen und bekannten Ansatz, den die Forscher als Normalisierungsmethode bezeichnen, werden die Erwartungswerte von Operatoren durch einfache Normalisierung mit der zeitabhängigen Norm des entsprechenden Quantenzustands berechnet. In Bezug auf die Zustandsentwicklung wird eine Übereinstimmung zwischen der metrischen und der Normalisierungsmethode nur dann gefunden, wenn die Nicht-Hermitizität sehr schwach ist; sobald die Nicht-Hermitizität relevant wird, entwickelt sich der Zustand in den beiden betrachteten Frameworks unterschiedlich, selbst wenn die PT-Symmetrie erhalten bleibt. Sim und Kollegen kommen zu dem Schluss, dass dies daran liegt, dass die Metrik eine wesentliche Rolle bei der Entwicklung des Quantenzustands spielt. Wenn das Team den Erwartungswert des Spin-Operators berechnet, findet es je nach gewähltem Framework auch unterschiedliche Werte. Nur bei der Metrik hat der Erwartungswert des Spins eine eindeutige Parität in Bezug auf den Impuls k; dieser Befund steht im Einklang mit einer zusätzlichen Charakterisierung der Symmetrie des Hamiltonians in den beiden Systeme, wo die Forscher eine analoge Diskrepanz feststellen.

Eingefrorenes Verhalten

Sim und seine Kollegen untersuchen als Nächstes, was passiert, wenn der angewandte Antrieb immer langsamer wird, was quantenmechanisch gesehen der adiabatischen Grenze entspricht. Sie definieren Defekte als Spin-Flips der Zwei-Niveau-Systeme, die sie von ihrem Ausgangszustand wegführen. Im metrischen Rahmen stellen sie fest, dass die Dichte dieser Defekte durch einen Beitrag ungleich Null charakterisiert ist, der ausschliesslich von jenen Zwei-Niveau-Systemen stammt, die spontane PT-Symmetriebrüche aufweisen. Das bedeutet, dass Defekte entstehen, egal wie langsam das System durch einen Ausnahmepunkt gefahren wird. Das Ergebnis stellt eine Verletzung der Quanten-Adiabatizität dar, ein Phänomen, das bereits in früheren experimentellen Studien beobachtet wurde: Im hermiteschen Standardfall tendiert die Dichte der Defekte im adiabatischen Grenzwert gegen Null. Die Forscher betonen, dass dieser Zusammenbruch der Adiabatizität, den sie als Defekt-Einfrieren bezeichnen, nur im metrischen Rahmen wiederhergestellt wird – die Arbeit mit der Normalisierungsmethode erfasst dieses ungewöhnliche Verhalten nicht.

Nach Ansicht von Sim und Kollegen ist der Effekt des Einfrierens von Defekten (oder sein Fehlen) eine Folge der Parität des Spin-Erwartungswerts, was wiederum bedeutet, dass die Metrik der entscheidende Faktor ist, der es ihnen ermöglicht, diese Eigenschaft des Systems zu erfassen, wenn sie es in ihrem metrischen Rahmen untersuchen. Die Verletzung der Quanten-Adiabatizität mag nicht so überraschend erscheinen, wenn man bedenkt, dass nicht-hermitesche Hamiltonoperatoren Systeme beschreiben, die von Natur aus nicht im Gleichgewicht sind. Dennoch deuten diese Ergebnisse darauf hin, dass sowohl im als auch ausserhalb des Labors noch mehr Arbeit geleistet werden muss, um die Rolle des metrischen Operators in Formulierungen der nicht-hermiteschen Quantenmechanik zu verstehen.

Aus dem Englischen übersetzt von Kilian Kessler